Table of Contents
Tutorial 1: Maze Branching
Author: Francis Palustre Email: palusf1@unlv.nevada.edu
Date: Last modified on <5/23/2024>
Keywords: Navigation, Data Structure, BFS, MATLAB
Motivation and Audience
This tutorial's motivation is to learn how to apply either Breadth-First Search (BFS) or Depth-First Search (DFS) to fully traverse in a maze and visit every possible space available. For this set of tutorials, BFS will be used. Readers of this tutorial assumes the reader has the following background and interests:
* Know how to read and understand pseudocode
* Know the basic understanding of how BFS and DFS work
* This tutorial may also attract readers who are interested in implementing algorithms in their own projects
The rest of this tutorial is presented as follows and should be possible to gain a suitable understanding in a of 2-3 hours:
Resources
The following resources are prerequisites to have a general understanding of the topic and is highly recommended to look and read the following links:
Breadth-First Search and Depth-First Search (DASL Wiki)
Breadth-First Search and Depth-First Search (2023) (DASL Wiki)
Breadth-First Search (GeeksForGeeks)
Breadth-First Search (Programiz)
Depth-First Search (GeeksForGeeks)
Depth-First Search (Programiz)
Methodology
Assuming you have a maze with known dimensions and walls, it is possible to apply either BFS or DFS to fully traverse the maze in its entirety. To do so, you can create small sub-rectangles of a certain length and width as nodes to represent the graph for the algorithms to follow.
The primary components to create this complex approach is the following in C++:
- Creating the Graph
- Tracker
- Inaccessible Nodes
- BFS or DFS (BFS in this method)
- Finding the Farthest Node
- A Path Accumulator (Queue)
The components can be written in Python as well, but with slight differences, The following components can be used to achieve similar results whilst implementing a stack and queue, rather that purely utilizing the latter:
- Creating the Graph
- BFS
- Finding the Farthest Node
- A Path Accumulator (Stack)
Note: It will be assumed that you have created the graph and the search algorithms as that is not specifically related to the application, rather a standard. Also, everything will be given in pseudocode because this following tutorials is used as a challenge rather than providing the answer.
Tracker
STRUCT CHANGER
counter <- integer
graph <- unordered_map
inaccessibleNodes <- unordered_set
END STRUCT
Inaccessible Nodes
FUNCTION add_inaccessibleNodes(node, change) currNode <- INTERATOR SET currNode TO INSERT node INTO change.inaccessibleNodes IF currNode IS TRUE THEN INCREMENT change.counter END IF END FUNCTION
Farthest Node
FUNCTION farthestNode(graph, startingNode, inaccessibleNodes) visited <- unordered_set que <- queue distance <- unordered_map farthestNode <- integer maxDistance <- integer currNode <- integer ADD startingNode TO visited ENQUEUE startingNode TO que SET distance[startingNode] TO 0 SET farthestNode TO startingNode SET maxDistance TO 0 //Base Case IF SIZE(graph) IS 1 THEN RETURN startingNode END IF //Non-base Case WHILE que IS NOT EMPTY DO SET currNode to DEQUE FOR EACH neighbor in graph[currNode] DO IF neighbor IS IN inaccessibleNodes THEN CONTINUE END IF IF neighbor IS NOT IN visited DO ADD neighbor TO VISITED ENQUEUE neighbor TO que SET distance[neighbor] TO distance[currNode] + 1 IF distance[neighbor] IS GREATER then maxDistance THEN SET maxDistance TO distance[neighbor] SET farthestNode TO neighbor END IF END IF END FOR END WHILE RETURN farthestNode END FUNCTION
Path Accumulator (C++)
FUNCTION pathAccumulation(change, startingNode, desiredNode) //change is a struct fullPath <- vector primaryPath <- vector SET primaryPath TO BFS(change.graph, startingNode, desiredNode, change.inaccessibleNodes) FOR EACH node IN primaryPath DO CALL add_inaccessibleNodes(node, change) END FOR FOR EACH primary_pathNode IN primaryPath DO ADD primary_pathNode TO fullPath FOR EACH adjNode in change.graph[primary_pathNode] DO IF adjNode IS NOT IN change.inaccessibleNodes THEN branchDesired <- integer SET branchDesired TO farthestNode(change.graph, adjNode, change.inaccessibleNodes) brachPath <- vector SET branchPath TO BFS(change.graph, adjNode, branchDesired, change.inaccessibleNodes) FOR EACH node IN primaryPath DO CALL add_inaccessibleNodes(node, change) END FOR reverseBranch <- vector SET reverseBranch TO branchPath REVERSE reverseBranch REMOVE FIRST ELEMENT FROM reverseBranch COMBINE branchPath AND reverseBranch COMBINE fullPath and branchPath END IF END FOR END FOR FOR EACH node IN fullPath DO CALL add_inaccessibleNodes(node, change) END FOR WHILE change.counter DOES NOT EQUAL TO SIZE(change.graph) DO index <- integer SET index TO 0 FOR EACH pathNode IN fullPath DO INCREMENT index FOR EACH adjNode in change.graph[pathNode] DO IF adjNode IS NOT IN change.inaccessibleNodes THEN branchDesired <- integer SET branchDesired TO farthestNode(change.graph, adjNode, change.inaccessibleNodes) brachPath <- vector SET branchPath TO BFS(change.graph, adjNode, branchDesired, change.inaccessibleNodes) FOR EACH node IN branchPath DO CALL add_inaccessibleNodes(node, change) END FOR reverseBranch <- vector SET reverseBranch TO branchPath IF SIZE(reverseBranch) IS LESS THAN OR EQUAL TO 1 THEN CALL add_inaccessibleNodes(adjNode, change) COMBINE fullPath + index WITH pathNode COMBINE fullPath + index WITH branchPath COMBINE fullPath + index WITH adjNode CONTINUE END IF REVERSE reverseBranch REMOVE FIRST ELEMENT FROM reverseBranch COMBINE branchPath AND reverseBranch COMBINE fullPath + index AND branchPath COMBINE fullPath + index AND pathNode END IF END FOR END FOR END WHILE RETURN fullPath END FUNCTION
Path Accumulator (Python)
FUNCTION pathAccumulation(graph, startingNode, removedNodes) furthestNode <- int primaryPath <- List SET furthestNode TO farthestNode(graph, startingNode, removedNodes) SET primaryPath TO BFS(graph, startingNode, furthestNode, removedNodes) finalPath <- List stack <- deque #best to use the deque module from collections FOR EACH node IN primaryPath ADD node TO finalPath ADD node TO stack WHILE stack IS NOT EMPTY currNode <- int SET currNode TO last index of stack added <- bool SET added TO FALSE FOR EACH adjNode IN graph[currNode] IF adjNode NOT IN primaryPath AND removedNodes AND finalPath AND stack ADD neighbor TO stack SET added TO TRUE IF added IS FALSE REMOVE LAST ELEMENT IF stack IS NOT EMPTY branchPath <- List SET branchPath to BFS(graph, currNode, stack[-1], removedNodes) SET AND ADD branchPath TO finalPath IF finalPath[-1] DOES NOT EQUAL TO node branchPath <- List SET branchPath to BFS(graph, finalPath[-1], node, removedNodes) SET AND ADD branchPath TO finalPath return finalPath END FUNCTION
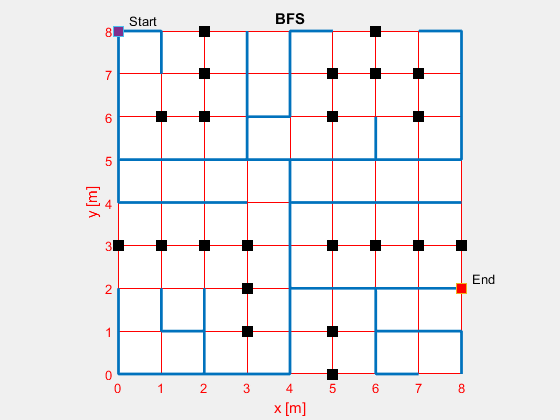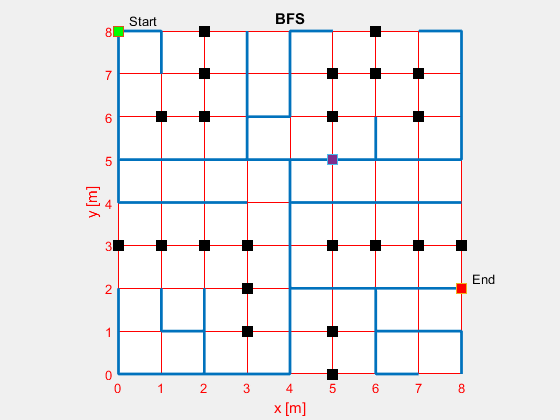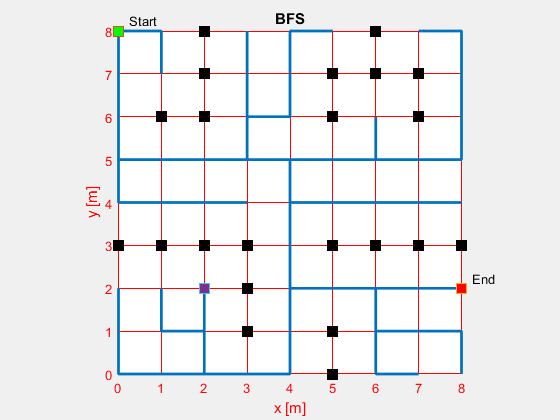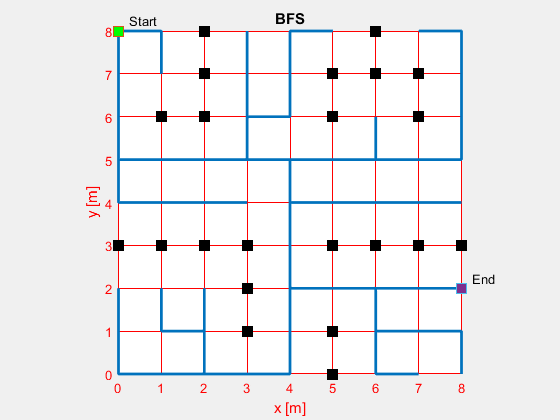
MATLAB Result
Once the code has been made, the output would be the desired path of your maze. To visually see it, the following is a MATLAB implementation of the queue version of the maze-branching algorithm.
- Green: Start Node
- Red: End Node
- Purpose: Navigator
- Black: Obstacles
- Blue: Path
Final Words
This tutorial's objective is how to potentially incorporate search algorithms in an applicative setting and to develop critical and creative thinking skills to improve one's coding skillset.
Speculating future work derived from this tutorial, includes learning and other algorithms such as Dijkstra and A* and apply it to robots and programs. In the big picture, the problem of applying search algorithms in the real-world can be solved with this tutorial.
For questions, clarifications, etc,
Email: palusf1@unlv.nevada.edu