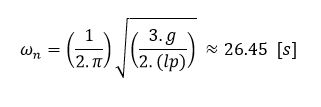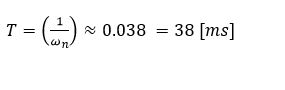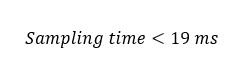PROGRAMMING THE BALANCE USING NQC LANGUAGE
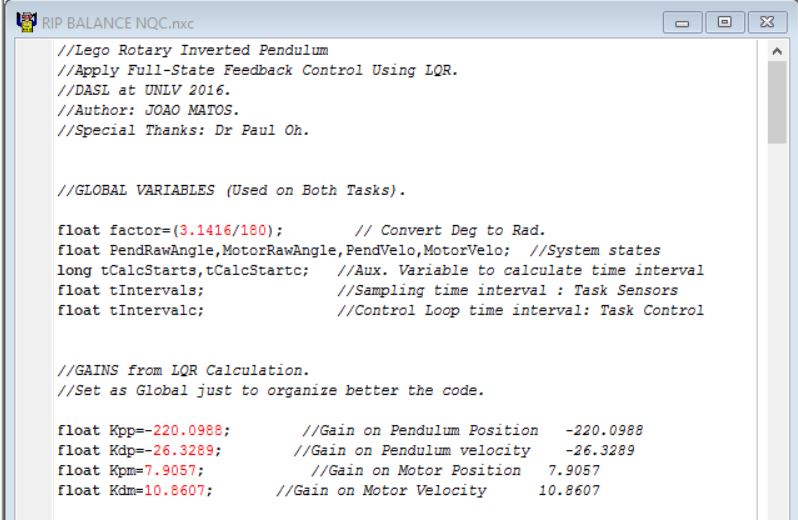
For this section ,use the gains that you find following the Modelling tutorial. As the model assumed some approximations , these gains can be tuned if needed. On my case i did not need any tunning after the calculation.
Following this tutorial you will be able to make the system balance like this:
Hardware and Software:
You will need a NXT Brick and the Bricx Command Center program.
Part I) Setting the global variables:
Here is declared the variables that are available to all tasks and functions at all time.On the Bricx Command Center ,to define a variable as global , it needs to be the first thing coded (declared before the functions and tasks).Actually , you will only know the variables that needs to be global while you are codding.
Part II) Setting the Auxiliary Functions:
The second thing to be coded are the user-defined functions.On the Bricx Command Center ,they need to be declared before the tasks.
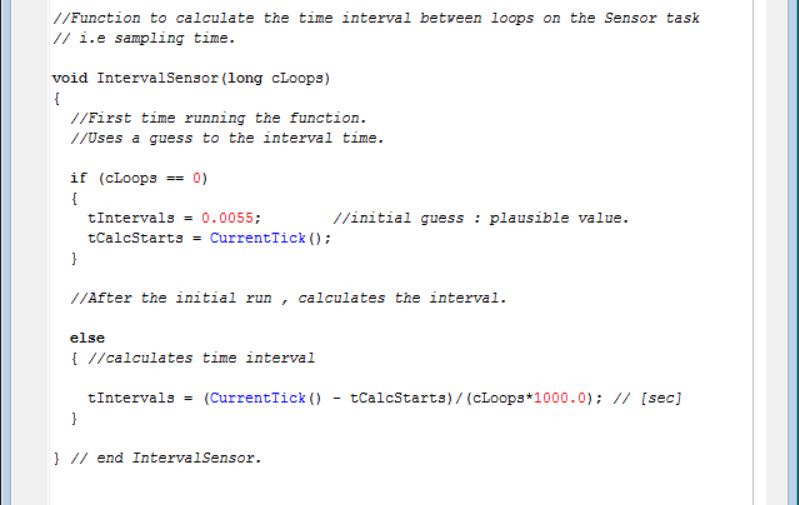
This two functions are used to calculate the interval between loops (Two because we will use two tasks - one to calculate and one to balance). It starts with an initial guess and then every time that they are called on the “while” loops inside each tasks , they will calculate the time interval between the loops ( time interval between two consecutive callings).
Part III) First Task: Getting the angles and calculating the velocities from the encoders:
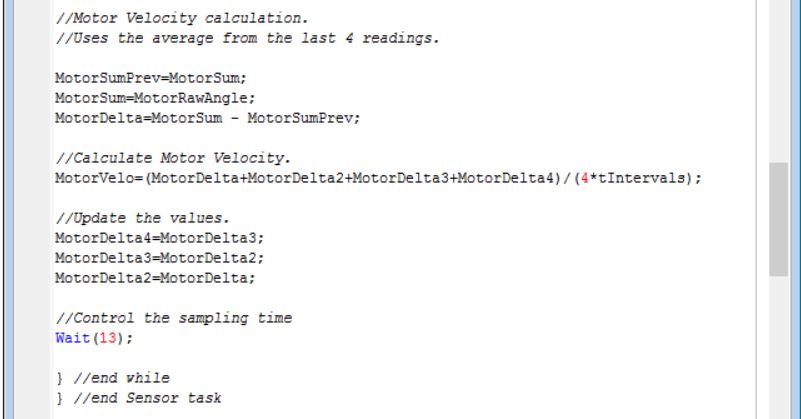
This tasks is used to calculate and store as global variables the pendulum and motor position and velocity. As we are using a Power Function XL- Motor , we need to connect it to a controller. Using the GlideWheel-M Motor Controller from mindsensors , we can easily get the position of the encoder using the same API's that are used for a regular Nxt Motor. Using “MotorRotationCount” we can get the position . And we can use some codding to estimate the velocity. First we get the Angle using the API, and then we convert it to radians . After, we can program the velocity to be calculated as the average from 4 previous values. The time interval used on the calculation is provided by the functions declared at Part II).
Is important to define your sampling time ( SEE SAMPLING TIME APPENDIX AT THE BOTTOM ). The “Wait()” statement at the end of this task will define your sampling time - which is a key thing to achieve a good balance.
Part IV) Starting the system and Controlling
The system starts with a 6 seconds count down on the screen. The Pendulum initial position needs to be at the bottom , and when you start the program , after 6 seconds the balance tasks will initialize.
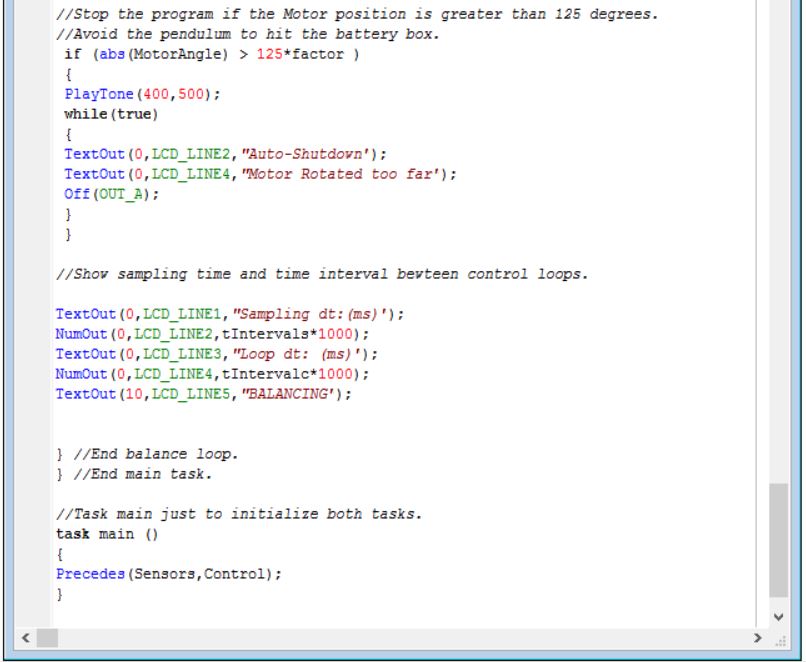
We can use an endless loop to keep calculating the motor input and send this value to the motor. First , some calculations needs to be done with the states calculated by the Sensor task. The motor position will be used as the actual position - initial position (to avoid any error on the position while the user swings the pendulum from the bottom to the top).As said on the state-space representation section,the pendulum starts from 180 degrees at the bottom and goes to 0 degrees at the top , and any position clock wise from 0 is a positive displacement and any position counter clock wise from 0 is a negative displacement.Using two conditional statement , the pendulum angle value can be normalized. The input to be send to the motor is calculated as the Gains multiplied by its related states , where the gains were previously calculated using Matlab (LQR). As the Lego motors only takes input from -100 to 100 another conditional statement can be used as a saturation. Your (+) direction marked on your GlideWheel should be the same as the direction of your OnFwd command .
SAMPLING TIME APPENDIX
Our system is a continuous time signal, and our code does not run continuously (it takes time to complete all the control loop and send the input to the motor). This way, we need to provide the continuous position and velocity of the motor and the pendulum to the control loop in a good “way”. The process to convert this continuous position of the motor and the pendulum to a discrete time signal is called Sampling. An easy way to understand the sampling is to think as the problem to define a continuous curve with a finite number of points. Following the Nyquist-Shannon sampling theorem we can estimate what sampling time can be good to discretize our model. The Frequency oscillation of our model is the Pendulum natural frequency, which can be calculated using:
The period of oscillation is the inverse of the natural frequency.
Our sampling time should be at least 2 times faster than the period of oscillation, but preferably 10 times faster. This way:
SEE FOR YOURSELF: Try to change the value of the “Wait” statement at the end of the Sensor Task and see what happens with the balance when your sampling time is not enough to provide a good discretization.