This is an old revision of the document!
Table of Contents
LEGO Rotary Inverted Pendulum Ver. 2.0
Modeling of the rotary inverted pendulum
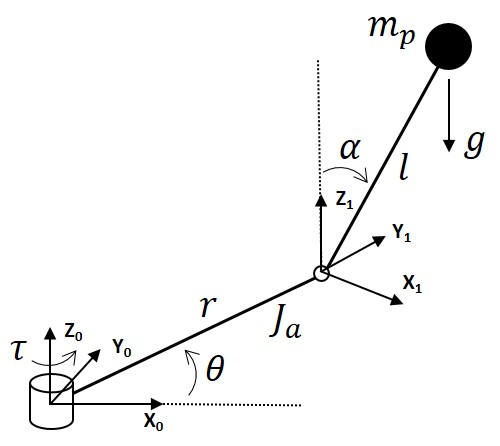
The rotary inverted pendulum has one motor on the base joint and two encoders on each joint.
The encoders measure angular displacements of a swing arm and a pendulum.
I assume that the joint friction and the viscous damping of the motor are neglected.
At a swing arm, r, Ja, θ, and τ are a link length, a moment of inertia of the swing arm, an angular displacement, and a joint torque, respectively. At a pendulum, l, mp, α, and g are a link length, a pendulum mass, an angular displacement, and gravity acceleration, respectively.
Equations of motion
Euler-Lagrange equation is used for derive equations of motion.
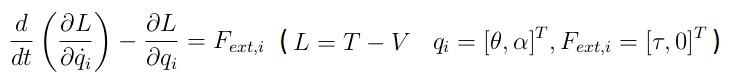
The kinetic energy of the system is
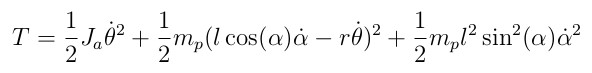
- HW. Derive the kinetic energy.
And the potential energy of the system is
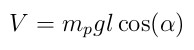
Then the Lagrangian is same as the following.
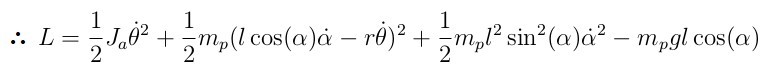
From Euler-Lagrange equation, the equations of motion are
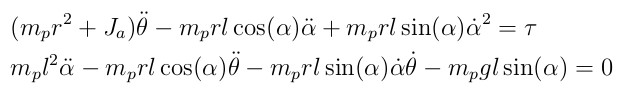
For linear control, we need to linearize the equations about near the equilibrium point (α = 0 ).
Assume that α is a small angle. Then,
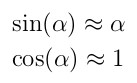
Therefore the linearized equations of motion are
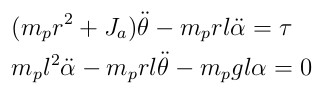
- HW. Linearize the above nonlinear equations by Taylor expansion.
For state-space representation, the equations are reconstructed.
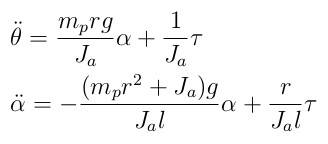
It needs to transform the input torque into the motor voltage because the torque can not be used by the input in the lego system. So the following DC motor model is needed to do that. If a motor inductance and viscous damping can be neglected,
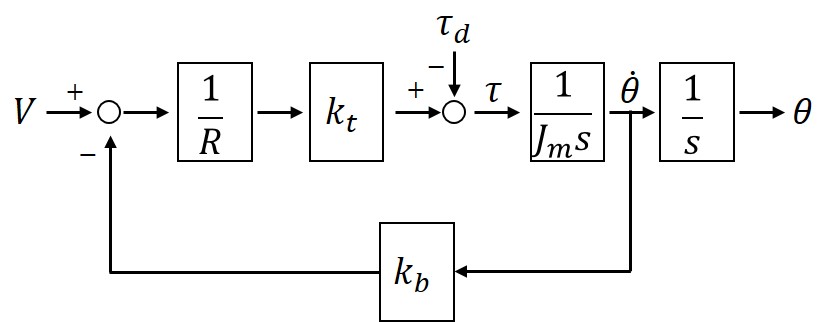
where, R, kt, Jm, and kb are a motor resistance, a torque constant, a motor armature inertia, and a back-emf constant, respectively.
Assume that an external torque is neglected and then the motor torque is
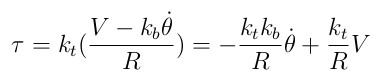
Let's substitute this motor torque into the equations of motion and set states X.
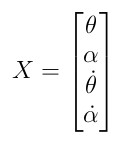
Therefore, the state-space representation for full-state feedback control is shown
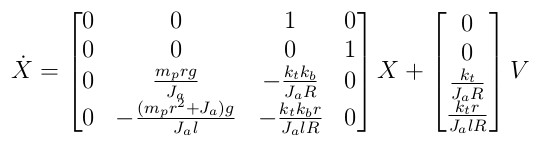
Full state feedback control
To control the LEGO RIP, a full state feedback controller is used.
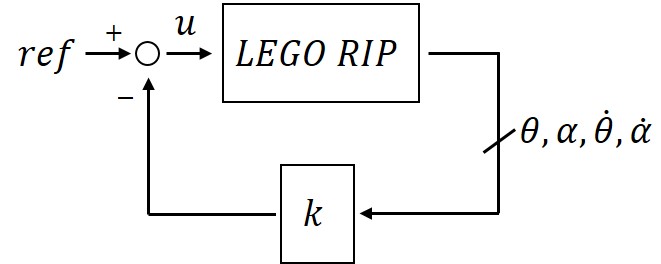
where, ref, k, and u are a reference input, a feedback gain vector, and a control input, respectively.
A control law is
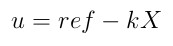
, and since we desire that the pendulum keeps upright, the ref is equal to zero.
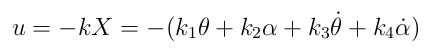
where k1, k2, k3, and k4 are gains of a swing arm angle, a pendulum angle, a swing arm angular velocity and a pendulum angular velocity.
Now we need to determine these gains.
LQR for the gains
<code> clear, clc, close all
mp=((2*0.36335)+(2*1.33192)+0.56)/1000; %Pendulum Mass r=140/1000; %Arm Length L=209/1000; %Pendulum Length g=9.81; %Gravity ma=(0.66556+1.33192)/1000; % Arm mass Ja=(1/3)*ma*(r^2); % Arm moment of inertia R=9.05; %DC-motor armature resistance kt=0.26; %DC-motor torque constant kb=0.26; %DC-motor back-emf constant
Am=[0 0 1 0;
0 0 0 1; 0 mp*r*g/Ja -kt*kb/Ja/R 0; 0 -(mp*r^2 + Ja)*g/Ja/L -kt*kb*r/Ja/L/R 0];
Bm=[0; 0; kt/Ja/R; kt*r/Ja/L/R];
q1 = 50; %Weight on motor position q2 = 50; %Weight on pendulum position q3 = 50; %weight on motor velocity q4 = 300; %weight on pendulum velocity
Q = diag([q1 q2 q3 q4]);
R = 1;
K =-lqr(Am,Bm,Q,R);
Gm_p=K(1,1); Gp_p=K(1,2); Gm_v=K(1,3); Gp_v=K(1,4); <\code>

