Table of Contents
Damped Compound Pendulum (DCP)
Author: Sangsin Park Email: sangsin80@gmail.com
Date: Last modified on <10/17/18>
Keywords: compound pendulum, pendulum control with a propeller, damped compound pendulum

The photo above depicts the damped compound pendulum (DCP) control which allows you to understand a second order system and PID control. The big picture problem is to make a good step response. Solving this partially or completely is important because a step response is a basis to analyze control performances. This tutorial shows you how to build a DCP system, how to find a relationship with control input voltages (i.e. analog output voltages as a base voltage of a transistor to rotate a motor) and pendulum angles from an encoder, how to match a mathematical model with experimental measurements, how to make a LabVIEW program for PID control, and experiments and takes approximately 2 - 3 hours to complete.
Additionally, LEGO DCP is included.
Motivation and Audience
This tutorial's motivation is to understand a second order system. Readers of this tutorial assume the reader has the following background and interests:
* Know how to control a plant
* Perhaps also know how to make equations of motion
* This tutorial may also attract readers who want to understand how to find a system ID
The rest of this tutorial is presented as follows:
- Parts List and Sources
- Construction
- Modeling
- System ID
- PID control
- Experiments
- LEGO DCP
- Final Words
Parts List and Sources
| PART NAME/DESCRIPTION | VENDOR | VENDOR Number or URL | PRICE (USD) | QTY |
|---|---|---|---|---|
| H5-360-IE-S/Optical Encoder | US Digital | https://www.usdigital.com/products/encoders/incremental/rotary/shaft/H5 | 92.95 | 1 |
| USB-6211/NI Multifuction I/O Device | National Instruments | http://www.ni.com/en-us/support/model.usb-6211.html | 949.00 | 1 |
| 1316.12.5/Glass fiber reinforced super nylon propeller | Graupner | https://www.graupner.com/Prop-12x5cm-5x2-Zol-l-/1316.12.5/ | 2.79 EUR | 1 |
| TIP31/NPN Transistor | RadioShack | https://www.radioshack.com/products/tip31-transistor | 1.50 | 1 |
| DC Motor/nominal voltage of 5V | - | - | - | 1 |
| Resistor/1k Ohms | - | - | - | 1 |
| Resistor/10k Ohms | - | - | - | 2 |
| Capacitor/10nF | - | - | - | 3 |
| 1N4004/zener diode | - | - | - | 1 |
| 4 pin connector | - | - | - | 2 |
| 3 pin connector | - | - | - | 1 |
Construction
This section gives step-by-step instructions along with photos to build circuits to drive a motor and read an encoder. There are circuits and devices what we need. Three schematics to construct a motor driver, connectors and low pass filters are shown following.

Step 1
Here are top and down pictures of a circuit of a motor driver and connectors. I use a socket which is placed between connectors for easy wire routing.

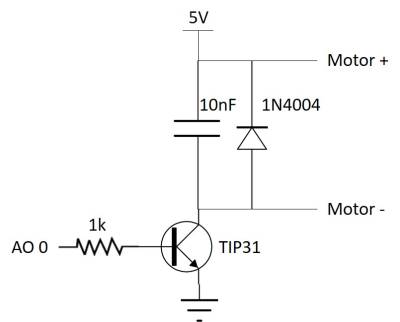
The schematics of the motor driver and the connectors are presented as follows. I use an NPN transistor (TR) to drive motor. As the base voltage of TR increases, the current through the motor increases. The encoder needs 5V and I use two signals of A and B to read the pendulum rotation angle. The connector #3 is for the USB-6211's analog output (AO) connection. Wires of AO GND and AO 0 are hooked up to the USB-6211's terminal 12 and 14, respectively.

Step 2
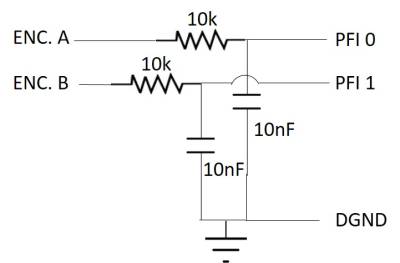
This is low-pass filters to get rid of the encoder's signal noise. The cut-off frequency is 1.59 kHz.

The schematic of the low-pass filter is presented as follows. A resistor of 10k ohms and a capacitor of 10 nF are used in it. Wires of PFI 0, PFI 1, and DGND are hooked up to the USB-6211's terminal 1, 2 and 5, respectively.
Step 3
Make sure that the USB-6211's wire connections are same as the picture.

Modeling
Free body diagram of DCP is presented as follow:
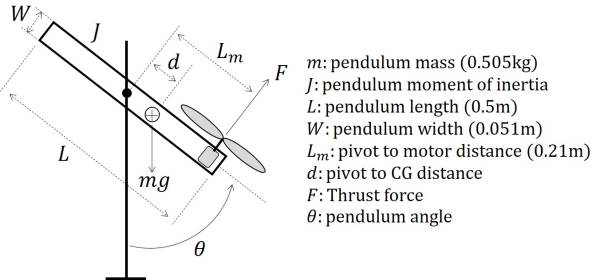 Equation of motion (EOM) is given by
Equation of motion (EOM) is given by
 and
and
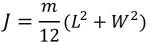 Assume that the pendulum moment of inertia is a plate about its center and the thrust force is proportional to the control input voltage which is the output voltage from USB-6211 (see the following figure). Let's set the ratio as Km.
Assume that the pendulum moment of inertia is a plate about its center and the thrust force is proportional to the control input voltage which is the output voltage from USB-6211 (see the following figure). Let's set the ratio as Km.
 Then the EOM can be rewritten by
Then the EOM can be rewritten by
 To find the Km, I use the steady-state behaviour of the DCP. At steady-state θss, angular velocity and acceleration go to zero. Therefore, the EOM is simplified by
To find the Km, I use the steady-state behaviour of the DCP. At steady-state θss, angular velocity and acceleration go to zero. Therefore, the EOM is simplified by
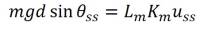 or,
or,
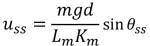 Try several experiments by choosing different values of AO voltage and measure the steady-state pendulum angles. The experiement results are shown in a following table.
Try several experiments by choosing different values of AO voltage and measure the steady-state pendulum angles. The experiement results are shown in a following table.
| AO Voltage (V) | Pendulum Angle (degree) |
|---|---|
| 0.8 | 0 |
| 0.85 | 2.25 |
| 0.9 | 4 |
| 0.95 | 5.75 |
| 1 | 8.5 |
| 1.2 | 16.5 |
| 1.4 | 26 |
| 1.6 | 34 |
| 1.8 | 43 |
| 2.0 | 51.5 |
| 2.2 | 64 |
| 2.4 | 78 |
From the experiment data, I can plot a graph such as
 Then, I use the first degree polynomial equation to fit to data points. The result is shown in
Then, I use the first degree polynomial equation to fit to data points. The result is shown in
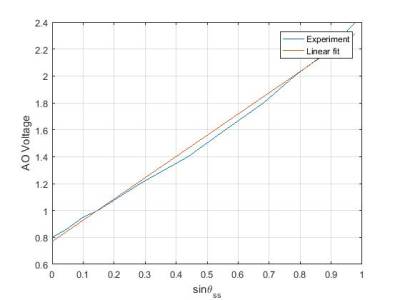 and the fitted polynomial equation is
and the fitted polynomial equation is
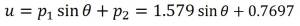 Note that DCP has a dead-zone which means that it needs greater than 5V to rotate a propeller, and the offset value of 0.7697 is used.
Now, the Km can be determined With the fitted polynomial equation
Note that DCP has a dead-zone which means that it needs greater than 5V to rotate a propeller, and the offset value of 0.7697 is used.
Now, the Km can be determined With the fitted polynomial equation

To linearize the EOM, assume that the pendulum angle is small. Then the value of sinθ is similar to θ.
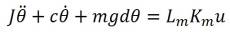 Taking Laplace transform, the transfer function of DCP would be
Taking Laplace transform, the transfer function of DCP would be
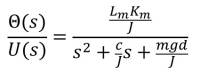 And, the block diagram of the above transfer function would be
And, the block diagram of the above transfer function would be

System ID
The unknowns of the DCP which are damping coefficient ( c ) and distance from pivot to CG (d) can be determined by system identification.
The DCP is the second order system and all second order system have the following characteristic equation.
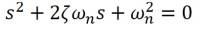 Moreover, there are two relationships.
Moreover, there are two relationships.
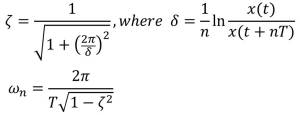 I use 10 degrees step response because of less oscillation time and pick out first two peak points to calculate damping ratio and natural frequency.
I use 10 degrees step response because of less oscillation time and pick out first two peak points to calculate damping ratio and natural frequency.
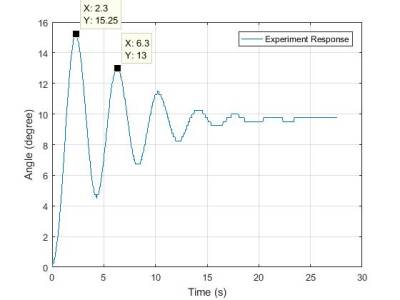 By the calculation, yields the following: ζ = 0.0127 and ωn = 1.5783.
The calculated damping ratio, however, is too small after comparing a model response with experiment response. To match two responses similarly, I add 0.085 to that value. Therefore, ζ = 0.0977.
The comparison with experiment and model response is shown in the following figure.
By the calculation, yields the following: ζ = 0.0127 and ωn = 1.5783.
The calculated damping ratio, however, is too small after comparing a model response with experiment response. To match two responses similarly, I add 0.085 to that value. Therefore, ζ = 0.0977.
The comparison with experiment and model response is shown in the following figure.

PID Control
A LabVIEW program is employed to control the DCP and PID controller is implemented on it at control frequency of 200Hz. The P, I, and D gain are 0.1, 0.28, and 0.9, respectively.
 In addition, there is the front panel of that LabVIEW block diagram.
In addition, there is the front panel of that LabVIEW block diagram.

Experiments
Before installing a propeller, make the propeller's hole bigger (see the following picture). I drill a hole of 5 mm but recommend a hole of 5.5 mm.
 Then, there is a motor assembled with the propeller.
Then, there is a motor assembled with the propeller.

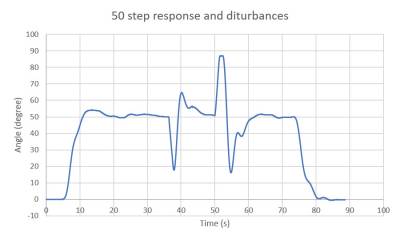
Exp. #1
Exp. #2
Gradually increase step commend from 40 to 65 degrees: 40, 50, 60, and 65 degrees.
And the experiment #2's graph is shown in

LEGO DCP
You can make a LEGO version DCP with LEGO bricks, a motorized propeller, and a HiTechnic angle sensor. Even if the angle sensor's resolution is not good (1-degree accuracy), a LEGO DCP control does not matter.

LabVIEW block diagram for PID control
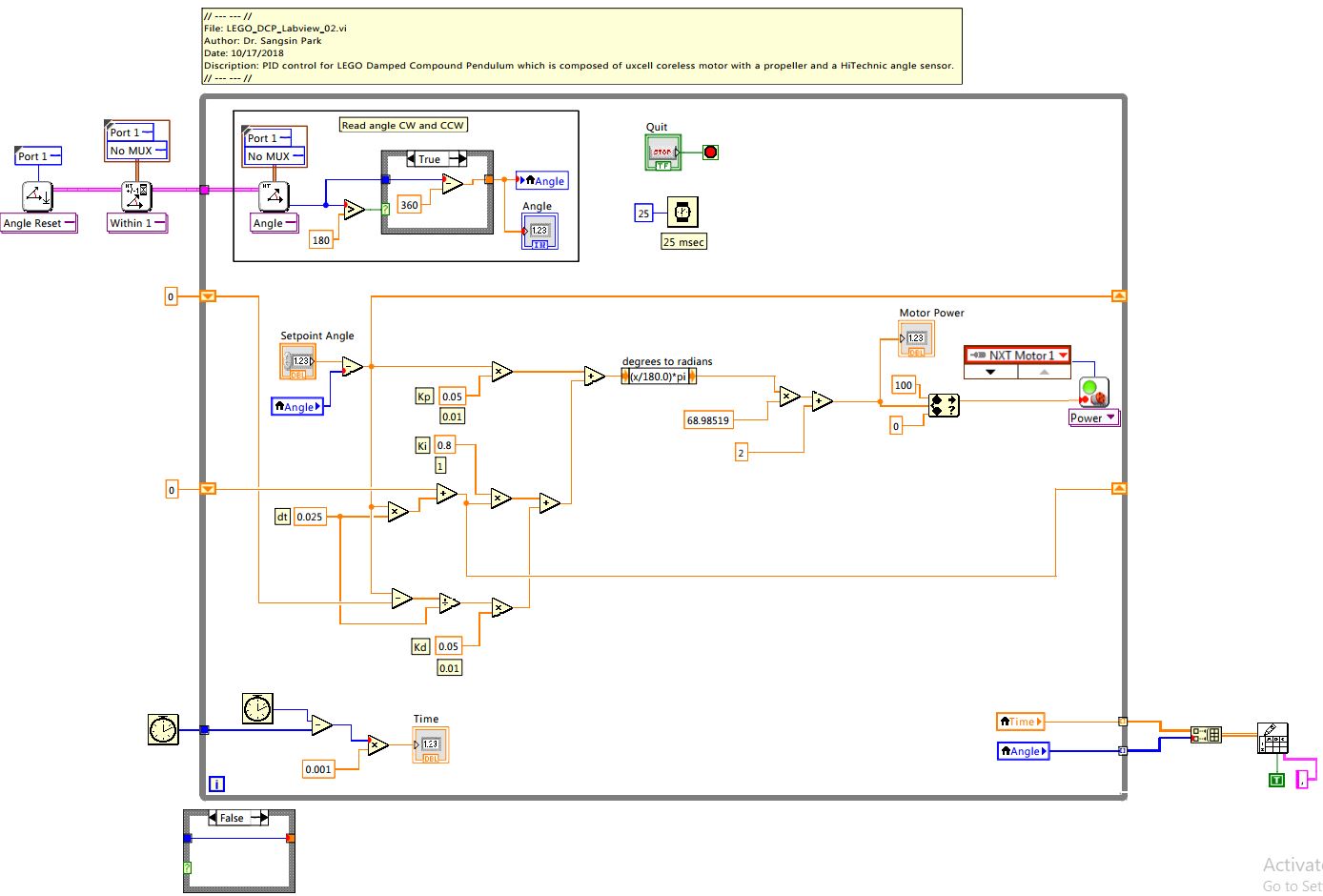
A LabVIEW program, which is similar to the before LabVIEW code, is employed to control the LEGO DCP at a control frequency of 40Hz. The P, I, and D gain are 0.05, 0.8, and 0.05, respectively.
Here is the LabVIEW file. lego_dcp_labview_02.zip
 In addition, here is the front panel of the LabVIEW program.
In addition, here is the front panel of the LabVIEW program.
A breakdown of the LabVIEW block diagram is shown as follows.
1. Initialize an angle sensor
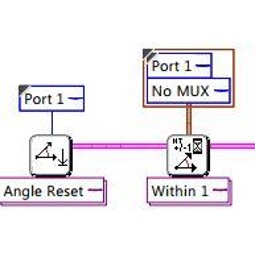 Before while loop, reset angle sensor and wait until its angle is within 1 degree.
Before while loop, reset angle sensor and wait until its angle is within 1 degree.
2. Read angle
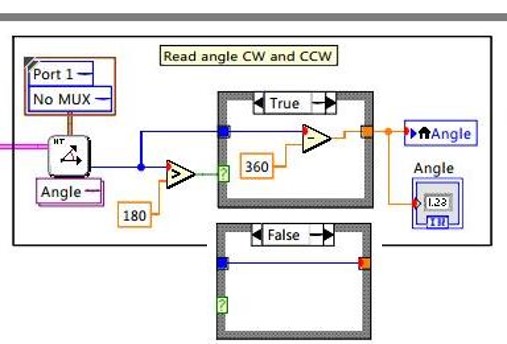 An angle from the angle sensor is measured in the range 0 to 359 degrees with 1-degree accuracy. To display angle in the range -180 to 180, when the angle is greater than 180, subtract 360 from that. Moreover, to avoid getting mixed up with wires, I assign a local variable for the Angle.
An angle from the angle sensor is measured in the range 0 to 359 degrees with 1-degree accuracy. To display angle in the range -180 to 180, when the angle is greater than 180, subtract 360 from that. Moreover, to avoid getting mixed up with wires, I assign a local variable for the Angle.
3. PID controller
 If a control frequency is changed, a value of dt also needs to be changed to a value of 1/frequency.
If a control frequency is changed, a value of dt also needs to be changed to a value of 1/frequency.
4. Convert angle to motor power
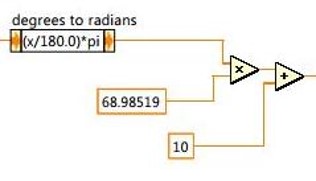 A constant of 68.98519 is a proportional gain to convert from angle to motor power and another constant of 10 is bias for dead-zone. Those constants can be determined by curve-fitting (see the Modeling section).
A constant of 68.98519 is a proportional gain to convert from angle to motor power and another constant of 10 is bias for dead-zone. Those constants can be determined by curve-fitting (see the Modeling section).
5. Input motor power
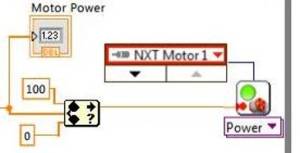 For safety and to limit motor rotation to a single direction, a motor power is constrained by in the range of 0 to 100.
For safety and to limit motor rotation to a single direction, a motor power is constrained by in the range of 0 to 100.
NB: If motor terminals are hooked up to an oscilloscope, a motor power range becomes strange. The motor power is in the range -100 to 100. Zero power is not zero anymore. For example, at -100, a motor doesn't rotate and at 0, it can rotate.
6. Save time and angle
 To calculate experiment time, read a current time before while loop, and then subtract the time from a time updated in while loop. Lastly, two local variables, Time and Angle, are written into a file after press a STOP button.
To calculate experiment time, read a current time before while loop, and then subtract the time from a time updated in while loop. Lastly, two local variables, Time and Angle, are written into a file after press a STOP button.
Exp. #1 - 40 degrees step command and disturbances
Final Words
This tutorial's objective is to understand a second order system through a compound pendulum with a motorized propeller referred to as Damped Compound Pendulum (DCP) and I share my efforts in detail regarding two different DCP realization. PID control of a DCP is successful and then a LEGO version DCP is made for control class and hands-on lab. Eventually, the LEGO DCP is also controlled well.
For questions, clarifications, etc, Email: sangsin80@gmail.com