MATLAB Program
Comparing the 4 bar mechanism and the LEGO model, we can see that the crank becomes the vector “W,” etc.

In Solidworks (details shown later), the 4 bar mechanism has the following measurements:

To model the 4 bar mechanism, the initial states of the 4 bar mechanism will be initialized in MATLAB, where the dimensions are as shown:
W1 = sqrt(2)/2*exp(i*-66*pi/180); V1 = 4*exp(i*93.85*pi/180); G1 = 5 + i*0; U1 = 6*exp(i*146.12*pi/180);
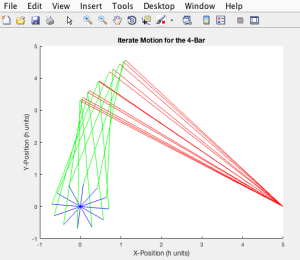
Then, determine the rotation cycle of the crank. Here, I want to crank to go through two cycles, therefore, I stopped at angle 360*2:
start_ang = 0; step_ang = 2; stop_ang = 360*2;
The rotational speed are determined according to the realistic motor data measured from the NXT, which is 89 RPM.
Then, the 6 state equations derived above are fed into the function “fsolve” such that for every movement of the crank (0, 2, 4, 6 … 360*2), all 6 equations are solved.
Using the fact that points a1, b0, b1 can be found like the following:
a1x(i) = W*cos(theta+beta)+a0x(i); a1y(i) = W*sin(theta+beta)+a0y(i); b0x = ones(N,1)*0+Gx; b0y = ones(N,1)*0+Gy; b1x(i) = U*cos(gamma+sigma)+b0x(i); b1y(i) = U*sin(gamma+sigma)+b0y(i);
a plot of the 4 bar mechanism cycle can be graphed in MATLAB.
Solving the 6 state equations will allow you to find the angular displacement, velocity, and acceleration variables:
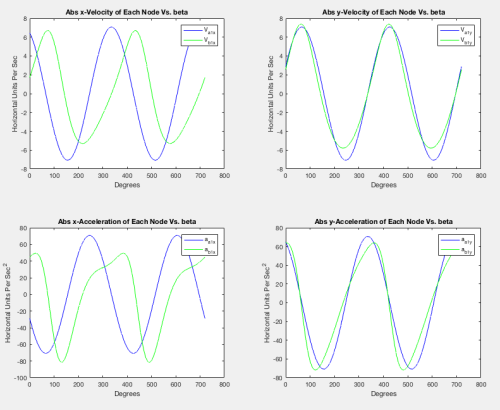
To solve for the linear velocity and linear acceleration variables, we use the following relationship:
da1_dtx(i) = -W*betap*sin(theta+beta); da1_dty(i) = W*betap*cos(theta+beta); dda1_dtx(i) = -W*betapp*sin(theta+beta)-W*betap^2*cos(theta+beta); dda1_dty(i) = W*betapp*cos(theta+beta)-W*betap^2*sin(theta+beta); db1_dtx(i) = dVdtx(i)+da1_dtx(i); db1_dty(i) = dVdty(i)+da1_dty(i); ddb1_dtx(i) = ddVdtx(i)+dda1_dtx(i); ddb1_dty(i) = ddVdty(i)+dda1_dty(i);

