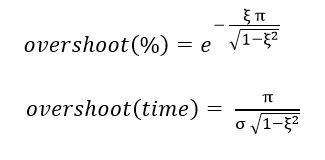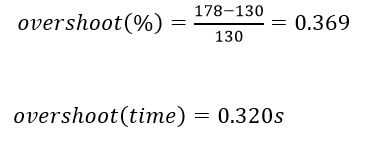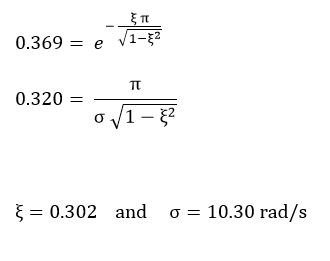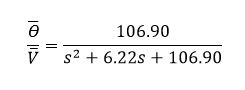This is an old revision of the document!
PID CONTROL
We can analyze the whole system into two distinct transfer functions , one for the ball and beam , and one for the motor. After , we can analyze the whole system putting these two transfer functions together in a block diagram.
Ball and Beam Transfer Function Derivation

Analyzing the equilibrium we have:
Motor Transfer Function Derivation
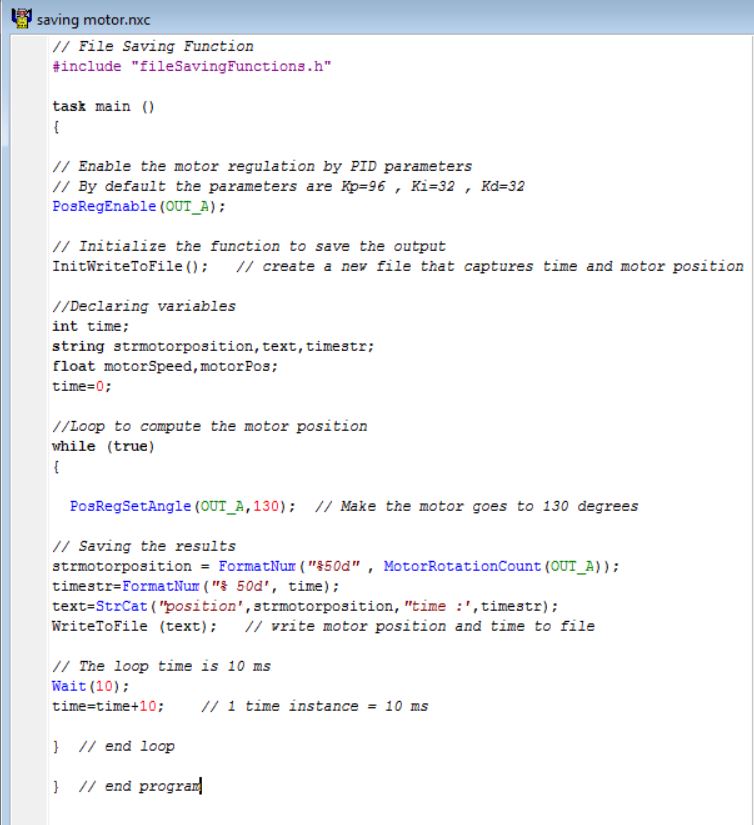
One easy way to get the motor's transfer function is to plot and analyze its response to an input , and by a graphical analysis get the parameters to derive its transfer function. We can program an algorithm to read and save ( using file saving functions ) the motor position during its operation. The following code was used to save and after plot the motor response until it get to the desired angle.The code makes the motor runs from 0 to 130 degrees, controlled by PID using the function “ PosRegEnable ” .
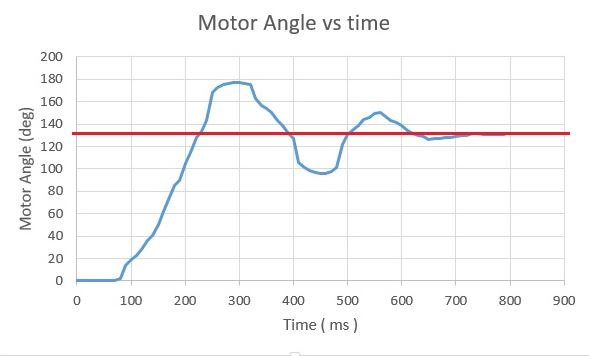
Plotting the results we have:
By the graphic response , we can assume the motor system as a second order system (because of the oscillatory and overshoot response). As known , a second order is characterized by two parameters , natural frequency (σ) and damping ratio (ξ).We can get these parameters by the following steps:
We know that a second order transfer function is:
So the motor's transfer function is: