Table of Contents
Ball and Beam v2
Motivation
The ball and beam system is also called ‘balancing a ball on a beam’.It is generally linked to real control problems such as horizontally stabilizing an airplane during landing and in turbulent airflow. There are two degrees of freedom in this system. One is the ball rolling up and down the beam, and the other is beam rotating through its central axis. The aim of the system is to control the position of the ball to a desired reference point, and reject disturbances such as a push from a finger. The control signal can be derived by feeding back the position information of the ball. The control power signal goes to the servo-motor,then the torque generated from the motor drives the beam to rotate to the desired angle. Thus, the ball can be located at the desired position.
It is important to point out that the open loop of the system is unstable and nonlinear. The problem of ‘instability’ can be overcome by closing the open loop with a feedback controller. The nonlinear property is not significant when the beam only deflects a small angle from the horizontal position. In this case, it is possible to linearize the system. However, the non-linearities become significant when the angle of the beam from the horizontal is larger than 30 degrees, or smaller than -30 degrees. In this case, a simple linear approximation is not accurate. Thus a more advanced control technique such as nonlinear control should work better.
Assumptions
In order to theoretically model the ball and beam system, the assumptions are listed in the following:
- The ball rolls on the beam without slip
- The gearbox embedded in the motor exhibit no backlash effect
- The base of the system is static with respect to the ground
- The beam is able to rotate between -30 degrees to 30 degrees relative to the horizontal
Design Solutions
The whole structure is made up of pieces of lego mindstorm kit ; There is a lego servo-motor that tilt the beam by using a wire, and the beam is hinged on the other side as shown the picture below.
Ball's position is detected by a Infrared distance sensor for NXT (DIST-Nx-v3)that is fixed on the beam.
Mathematical Model
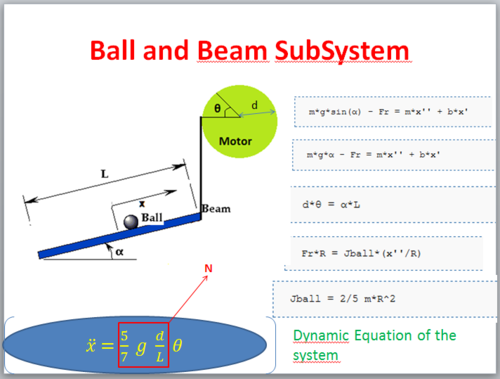
According to physics laws, mathematical equations are derived to model a system. Therefore, a detailed derivation of those equations is presented. The following equation can be derived from analysis of the force balance on the ball employing Newton’s law.
m*g*sin(α) - Fr = m*x'' + b*x'
where m is the mass of the ball, g is acceleration of gravity, x is the vertical distance between the center of ball and center of the shaft, b1 is the friction constant while the ball rolls on the channel of the beam, α is the beam’s tilt angle from the horizontal position, Fr represents the externally applied force.
Based on the small angle theorem, this relation can be approximated by in the form:
m*g*α - Fr = m*x'' + b*x'
The angle of the beam α is linked to the angle of the motor θ according the following equation:
d*θ = α*L
where d is the radius of the pulley and L is the length of the beam;
The torque balance of the ball is expressed as:
Fr*R = Jball*(x''/R)
where x is the linear acceleration of the ball, Jball is the moment of inertia of the ball, given by:
Jball = 2/5 m*R^2
Finally, the following result can be derived (neglecting the friction constant b1):
(m*g*d*θ)/L = (m + Jball/(R^2))*x''
Control
The open loop of the system is unstable so it can be overcome by closing the open loop with a feedback controller.
The error between set point and current position of the ball must be handled before being sent to the system, and this will be the task of the PID control:
The control signal is thus a sum of three terms: the P-term(which is proportional to the error), the I-term(which is proportional to the integral of the error), and the D-term(which is proportional to the derivative of the error). The controller parameters are proportional gain Kp, integral gain Ki, and derivative gain Kd. The integral, proportional and derivative part can be interpreted as control actions based on the past, the present and the future. Two controllers must be developed to control this system: an angular position controller for the motor controlling beam angle and a controller for the ball position and velocity on the beam. For this project, a stock controller available through the NXC programing language was used to control the motor position. This controller uses Proportional-Integral-Derivative (PID) control to set a motor position with an appropriate rise time and minimal overshoot of the set value. This controller can be accessed in two ways. One way allows the PID gains to be set manually. The second way (used in the following controller code) allows the user to control the maximum motor velocity and acceleration effectively dampening the system.
To control ball position and velocity it will be used a PD control because theoretically there isn't a steady state error and then Ki will be useless.
Motor Position Control
For PID control of the NXT motor on Port A:
code c> OnFwdRegPID(byte outputs,
char pwr, byte regmode, byte p, byte i, byte d )
</code>
For Velocity and Acceleration control of the NXT motor on Port A:
PosRegEnable(OUT_A); PosRegSetMax(byte output, byte max_speed, byte max_acceleration ) PosRegSetAngle (OUT_A, angle);
The angular position of the motor is accessed via a built in encoder using the following command:
curAngleInDegrees = MotorRotationCount(OUT_A);
Ball Position and velocity Control
To control the ball on the beam it is required the use of a sensor that is able to recognize the current position of the ball so “High Precision Medium Range Infrared distance sensor for NXT (DIST-Nx-Medium-v3)” was chosen from Mindsensors.com
Documentation and examples for using this sensor can be found on their website.
SetSensorLowspeed(S1); DISTNxSendCommand(S1, DIST_CMD_ENERGIZED, DIST_ADDR); DR = DISTNxReadValue(S1, DIST_REG_DIST_LSB, 2, DIST_ADDR); //Read Sensor Value
The current position of the ball will be compared with the set point in order to give the error that will be managed by the PD controller. In order to understand the accuracy of the sensor, two tests were performed:
1) the ball is stack on the central position of the beam:
where Error is the difference between the set point (the central position) and the current position of the ball (now it is stuck).
2) the ball goes from the central position to one side of the beam:
Finally it is possible to understand that the sensor accuracy is very good.
Set Point
The PD controller needs an error between the current position of the ball (given by the sensor) and the set point. Before the control loop started, the sensor detects the central position of the ball in order to save the set point of the close loop; This was done by taking the average of many readings (ReadNum = 30) to calculate it.
float Error; float set_point; int ReadNum = 30; int i; ... for (i = 0; i < ReadNum; i++) //cycle for calibration { set_point += DISTNxReadValue(S1, DIST_REG_DIST_LSB, 2, DIST_ADDR); Wait(100); TextOut(10, LCD_LINE3, "Calibrating..."); } set_point = set_point/ReadNum; Error = DISTNxReadValue(S1, DIST_REG_DIST_LSB, 2, DIST_ADDR) - set_point; // give the Error = current position - set point
Filtering
To improve the quality of sensor data, a very simple filter has been implemented. Before sending the signal to the controller, the sensor reads 3 times the current position of the ball provided an average reading.
int FiltNum = 3; int j; ... Error = 0; for (j = 0; j < FiltNum; j++) { Error += DISTNxReadValue(S1, DIST_REG_DIST_LSB, 2, DIST_ADDR)- set_point; } Error = Error/FiltNum; // current error
Sensor Data
In order to understand what happens on the field, the sensor data was written on two files and was plotted on Matlab:
byte fileHandle1; short fileSize1; short bytesWritten1; byte fileHandle2; short fileSize2; short bytesWritten2; int t0; int time; ... DeleteFile("Tempo.txt"); DeleteFile("Data.txt"); CreateFile("Tempo.txt", 10000, fileHandle1); CreateFile("Data.txt", 10000, fileHandle2); t0 = CurrentTick(); X = Error ; // current error X //write on file time and error time = CurrentTick()-t0; string tmp1 = NumToStr(time); WriteLnString(fileHandle1,tmp1, bytesWritten1); string tmp2 = NumToStr(X); WriteLnString(fileHandle2,tmp2, bytesWritten2);
Controller
The error found as the difference between the set point and the current position of the ball is processed by the PD controller in order to send a command to the motor. The Kp and Kd gains were chosen by trial, error and observation. Before Kp were chosen in order to give stability to the system, and after Kd were chosen in order to reduce oscillations: use Kp to decrease the rise time and Kd to reduce overshoot and settling time.
float X float DerX floar X_old; float dT = 0.1; float angle; ... //PD control DerX = (X - X_old)/dT; // derivative error integral = integral + 1/2 *(X + X_old)*dT; // integral error (useless) angle = (Kp*X) + (Kd*DerX) + (Ki*integral); // command for motor after PD regulation PosRegSetAngle (OUT_A, -angle); // command for the motor X_old = X; //save current error
Video
Code
- BallandBeamv2.nxc
#include "dist-nx-lib.nxc" // Range Finder Device Address #define DIST_ADDR 0x02\ // 0.5 1.5 #define Kp 0.92 // non superare 1.1 (0.9) -92 #define Kd 0.40 // 0.40 #define Ki 0 byte fileHandle1; short fileSize1; short bytesWritten1; byte fileHandle2; short fileSize2; short bytesWritten2; float set_point=0; float X; long curAngleInDegrees; float Error; float X_old=0; float DerX; float integral=0; float angle; float dT = 0.1; int t0; int time; int ReadNum = 30; // number of mesures for sensor calibration int FiltNum = 3; // number of mesures read by the sesor during regolation int i; int j; task main() { DeleteFile("Tempo.txt"); DeleteFile("Data.txt"); CreateFile("Tempo.txt", 10000, fileHandle1); CreateFile("Data.txt", 10000, fileHandle2); SetSensorLowspeed(S1); // empower the port 1 for sensor PosRegEnable(OUT_A); // empower the port A for motor DISTNxSendCommand(S1, DIST_CMD_ENERGIZED, DIST_ADDR); // energize the sensor for (i = 0; i < ReadNum; i++) //cycle for calibration { set_point += DISTNxReadValue(S1, DIST_REG_DIST_LSB, 2, DIST_ADDR); Wait(100); TextOut(10, LCD_LINE3, "Calibrating..."); } set_point = set_point/ReadNum; // give the set point Error = DISTNxReadValue(S1, DIST_REG_DIST_LSB, 2, DIST_ADDR)- set_point; // give the error DR_old = current position - set point t0 = CurrentTick(); while (1) { //cycle for regulation Error = 0; for (j = 0; j < FiltNum; j++) { Error += DISTNxReadValue(S1, DIST_REG_DIST_LSB, 2, DIST_ADDR)- set_point; } Error = Error/FiltNum; // current error X = Error ; // current error X //write on file time and error time = CurrentTick()-t0; string tmp1 = NumToStr(time); WriteLnString(fileHandle1,tmp1, bytesWritten1); string tmp2 = NumToStr(X); WriteLnString(fileHandle2,tmp2, bytesWritten2); // write on nxt display curAngleInDegrees = MotorRotationCount(OUT_A); // give the current angle of the motor in degrees (encoder) ClearScreen(); /*NumOut(0, LCD_LINE1, DR, false);*/ /*NumOut(0, LCD_LINE2, DR, false); */ NumOut(0, LCD_LINE4,Kp*X, false); /*NumOut(0, LCD_LINE6, dT, false);*/ NumOut(0, LCD_LINE7, Kd*DerX, false); NumOut(0, LCD_LINE8, curAngleInDegrees, false); //PD control DerX = (X - X_old)/dT; // derivative error integral = integral + 1/2 *(X + X_old)*dT; // integral error (useless) angle = (Kp*X) + (Kd*DerX) + (Ki*integral); // command for motor after PD regulation PosRegSetAngle (OUT_A, -angle); // command for the motor X_old = X; //save current error } DISTNxSendCommand(S1, DIST_CMD_DEENERGIZED, DIST_ADDR); // deenegize the sensor }
Cosiderations
The picture above shows how does PD control work. The PD control is enough stable and the ball reach the central position in a few seconds but there is a problem when the ball is close to steady state (central position in the beam). This might be due to reasons of structural type (stiffness of the structure or the presence of backlash in the internal gear box) or to problems related to the type of control.
Possible Solutions
First of all it was increasing the structural stiffness with a new support:
The vibrations of the building are greatly reduced but the problem is still present.
A new controller : the Linear Quadratic Regulator
A state space model of a typical plant is given by:
xdot = A*x + B*u
y = C*x + D*u
where A is the state matrix, B is the input matrix, C is the output matrix, D is the direct transmission matrix, x is the plant states, y is the output of the plant, and u is the vector of input signals.
The LQR stands for Linear Quadratic Regulator, which seeks a gain matrix that minimizes some performance index J:
J = ∫ [x'(t)*Q*x(t) + u'(t)R*u(t)]dt
where Q is the state weighting matrix, and R is the control weighting matrix. The optimal gain matrix is calculated by following Equation:
K = R^-1*B'*P
where P is determined by solving the algebraic Riccati Equation, show in following:
A'*P + P*A - P*B*R^-1*B'*P + Q=0
It is important to note that 'a unique, positive definite solution P, which minimizes the performance index J', can be determined by last equation, given that the system is controllable.
Mathematical Model
It is very important to find a mathematical model very close to real system for implementing a good LQR. The system can be divided into two subsystems in order to find transfer function from input (power to the motor) to output (ball position).
I system : motor identification
In some cases, plants or systems are so complicated or unknown that dynamics cannot be derived using simple physical laws. Therefore, it is necessary to use other methods to identify mathematical models of those systems. Inputs and outputs of the system have been measured through experiments. With this data, a system identification technique can be used to estimate both structures and parameters of the system.
In order to understand the transfer function from input power and angular speed of the motor, a plot of the step response of the motor (-30% of max power) is shown in the picture; Observing the response, it is possible to assume a I order for the motor system and finally calculate the characteristic parameters:
II system : ball and beam
In this second subsystem it is possible the use of dynamic equations as was shown in the previous section which are summarized in this picture :
Finally the transfer function of this two subsystem are used to build a good mathematical model of the ball and beam system; Matlab gives the possibility to compare the model with real system in order to understand its goodness;
In order to understand the power and efficacy of LQR control, I'm going to compare it with a PD control in order to show advantages.
PD CONTROL (PosRegSetAngle)
The Ball and Beam is a MIMO system because a motor position regulator is required for ball position control. Therefore, for PD simulation, I used a specific function called PosRegSetAngle in order to use an internal microcontroller (PID) of servomotor; In this way I can make a PD control of the ball position by introducing a second system identification on the system motor+internalcontroller:
Simulation with Simulink
By using Simulink, it is possible to compare actual system with a simulated system that is build from the dynamic equations writing before.
In order to obtain all system parameters, a Matlab code was running before simulation :
clc; close all; clear all; tos= 0.24; os= 8/30; R =0.020; %radius of the ball (m) m = 0.0026; %mass of the ball (kg) psi = sqrt((log(os)*log(os))/((log(os)*log(os))+(pi*pi))); %damping ratio (rad/s) sn = 1/(tos*sqrt(1-psi*psi)/pi); %natural frequency g = 9.8; %gravitational accelaration L = 0.645; %lenght of the beam (m) d = 0.015; % motor radius Jball = (2/5)*(m*(R^2)); %moment of inertia of the ball N = (m * g * d / L)/(m + (Jball/(R^2)));
NXC code for PD control
ATTENTION : before running the following code, place the beam in horizontal position and the ball close to the IR sensor ( 5 cm from it) in order to simulate a disturbance rejection (for more details see the video and observe the initial position of the beam and of the ball)
- PDControl.nxc
#include "dist-nx-lib.nxc" // Range Finder Device Address #define DIST_ADDR 0x02\ // 0.5 1.5 #define P 96 #define I 75 #define D 39 byte fileHandle1; short fileSize1; short bytesWritten1; byte fileHandle2; short fileSize2; short bytesWritten2; byte fileHandle3; short fileSize3; short bytesWritten3; byte fileHandle4; short fileSize4; short bytesWritten4; byte fileHandle5; short fileSize5; short bytesWritten5; float set_point=0.0; float Kp = 450; //from simulation float Kd = 450; float Ki = 0; float X; float curAngleInDegrees; float curAngleInDegreesOld=0.0; float CurPos; float vel; float thetam = 0.0; float X_old=0; float DerX; float integral=0; long angle; float r = 0.0; float dT = 0.1; float t0; float time = 0.0; float time_old; int ReadNum = 30; // number of mesures for sensor calibration int FiltNum = 3; // number of mesures read by the sesor during regolation int i; int j; task main() { DeleteFile("Tempo.txt"); DeleteFile("Data.txt"); DeleteFile("LinVel.txt"); DeleteFile("Theta.txt"); DeleteFile("AngVel.txt"); CreateFile("Tempo.txt", 1000, fileHandle1); CreateFile("Data.txt", 1000, fileHandle2); CreateFile("LinVel.txt", 1000, fileHandle3); CreateFile("Theta.txt", 1000, fileHandle4); CreateFile("AngVel.txt", 1000, fileHandle5); SetMotorRegulationTime (10); PosRegEnable(OUT_A,P,I,D); PosRegSetMax (OUT_A, 0, 0); SetSensorLowspeed(S1); // empower the port 1 for sensor DISTNxSendCommand(S1, DIST_CMD_ENERGIZED, DIST_ADDR); // energize the sensor for (i = 0; i < ReadNum; i++) //cycle for calibration { set_point = set_point + DISTNxReadValue(S1, DIST_REG_DIST_LSB, 2, DIST_ADDR); Wait(100); TextOut(10, LCD_LINE3, "Calibrating..."); } ClearScreen(); set_point = ((set_point/ReadNum)*0.001) + 0.2; // give the set point float dato = 0.0; long theta = 0; float AngVel = 0.0; float LinVel = 0.0; float xapCur = 0.0; float xaCur = 0.0 ; float u = 0.0; char Pwr; float time_old = 0.0; float thetaOld = 0.0; float CurPosOld = DISTNxReadValue(S1, DIST_REG_DIST_LSB, 2, DIST_ADDR)*0.001 - set_point; float CurPos = 0.0; float xapOld = 0.0; t0 = CurrentTick(); while (1) { //cycle for regulation for (j = 0; j < FiltNum; j++) { CurPos = CurPos + DISTNxReadValue(S1, DIST_REG_DIST_LSB, 2, DIST_ADDR)*0.001 - set_point; } CurPos = CurPos/FiltNum; // current error X = CurPos ; //write on file time and error time = (CurrentTick()-t0) * 0.001; theta = MotorRotationCount(OUT_A); thetam = theta * 0.0175 ; AngVel = (thetam - thetaOld)/(time - time_old); LinVel = (CurPos - CurPosOld)/(time - time_old); u = -1 * (Kp*CurPos + Kd*LinVel); ClearScreen(); NumOut(0, LCD_LINE1, u, false); NumOut(0, LCD_LINE2, CurPos, false); NumOut(0, LCD_LINE3, AngVel, false); PosRegSetAngle(OUT_A,u); Pwr = MotorActualSpeed (OUT_A); string tmp1 = NumToStr(time); WriteLnString(fileHandle1,tmp1, bytesWritten1); string tmp2 = NumToStr(X); WriteLnString(fileHandle2,tmp2, bytesWritten2); string tmp3 = NumToStr(Pwr); WriteLnString(fileHandle3,tmp3, bytesWritten3); string tmp4 = NumToStr(theta); WriteLnString(fileHandle4,tmp4, bytesWritten4); string tmp5 = NumToStr(Pwr); WriteLnString(fileHandle5,tmp5, bytesWritten5); time_old = time; thetaOld = thetam; CurPosOld = CurPos; xapOld = xapCur; CurPos = 0.0; } DISTNxSendCommand(S1, DIST_CMD_DEENERGIZED, DIST_ADDR); // deenegize the sensor }
Video and Plot
Finally we start simulation and real experiments with NXT and we can see how system react to a disturbance on ball position ( x0 = -0.2 m):
LQR CONTROL
Before applying the LQR system is necessary to convert the transfer function, previously identified, into the state space configuration. A possible state space representation can be :
Xdot = A*X + B*u Y = C*X + D*u
where X is the state vector which consisting of :
x1 = x = ball position
x2 = xdot = ball linear velocity
x3 = theta = angular position of the motor
x4 = thatadot = angular velocity of the motor
u is the input command (% duty cycle) and the matrices are:
A = [ 0 1 0 0 0 0 N 0 0 0 0 1 0 0 0 -1/tau ]
B = [ 0 0 0 -k/tau ]
C = [ 1 0 0 0 0 0 1 0 ]
D = [ 0 0 ]
where :
N = (m*g*d/L)/(m + (Jball/ (r^2)))
tau = time constant of the motor
k = steady state constant of the motor
Matlab & Simulink simulation
In order to solve the Riccati equation and find the vector of gains K, it is helpful the use of Matlab code:
clc; close all; clear all; % Iordine.m % this code find the K gains for Simulink model using "lqr" command % Antonio Tota tau= 0.34-0.120; k = 0.1750; R =0.020; %radius of the ball (m) m = 0.0026; %mass of the ball (kg) g = 9.8; %gravitational accelaration L =0.645; %0.390; %lenght of the beam (m) d = 0.015; % motor radius Jball = (2/5)*(m*(R^2)); %moment of inertia of the ball N = (m * g * d / L)/(m + (Jball/(R^2))); A = [0 1 0 0; 0 0 N 0; 0 0 0 1; 0 0 0 -1/tau]; B = [0; 0; 0; k/tau]; C = [1 0 0 0;0 0 1 0]; D = [0;0]; Cm = eye(4); Dm = [0;0;0;0]; Control = ctrb(A,B); Observe = obsv(A,C); controllability = rank(Control); Observability = rank(Observe); Tc = 0.054; %10 ms ts = ss(A,B,C,D); sysd = c2d(ts,Tc); Control1 = ctrb(sysd.a,sysd.b); Observe1 = obsv(sysd.a,sysd.c); controllability1 = rank(Control1) Observability1 = rank(Observe1) poles = eig(A) tsi = 5; %s desired settling time x1max = 0.01; %m max overshoot desired x2max = 0.3; %m/s x3max = 6.6904; %rad max motor angle desired(10° of the beam is good for linearization!!) x4max = 15; %rad/s (max angular speed of motor) umax = 50; %%dc max desired input ro = 100; %according Bryson's Rule, this is the tradeoff between control and energy (input) effort %according Bryson's Rule : Q = [1/(tsi*(x1max^2)) 0 0 0 ; 0 1/(tsi*(x2max^2)) 0 0 ; 0 0 1/(tsi*(x3max^2)) 0 ; 0 0 0 1/(tsi*(x4max^2)) ]; RR = ro/(umax^2) ; K = lqr(A,B,Q,RR) KK=dlqr(sysd.a,sysd.b,Q,RR) sim ('lqrfinalidI.mdl')
Finally, the gains obtained with “lqr” command are used for the following Simulink model:
NXC code for LQR control
ATTENTION : before running the following code, place the beam in horizontal position and the ball close to the IR sensor ( 5 cm from it) in order to simulate a disturbance rejection (for more details see the video and observe the initial position of the beam and of the ball)
After simulation, It's time to test the real system by using NXC code: Required Library File: dist-nx-lib.nxc
- LQRControl.nxc
#include "dist-nx-lib.nxc" // Range Finder Device Address #define DIST_ADDR 0x02\ // 0.5 1.5 #define P 96 // useless #define I 75 // useless #define D 39 // useless byte fileHandle1; short fileSize1; short bytesWritten1; byte fileHandle2; short fileSize2; short bytesWritten2; byte fileHandle3; short fileSize3; short bytesWritten3; byte fileHandle4; short fileSize4; short bytesWritten4; byte fileHandle5; short fileSize5; short bytesWritten5; float set_point=0.0; float K1=459.1388; float K2=594.0909; float K3=5.3849; float K4=0.4687; float X; float curAngleInDegrees; float curAngleInDegreesOld=0.0; float CurPos; float vel; float thetam; float X_old=0; float DerX; float integral=0; long angle; float r = 0.0; float dT = 0.1; float t0; float time=0.0; float time_old; int ReadNum = 30; // number of mesures for sensor calibration int FiltNum = 3; // number of mesures read by the sesor during regolation int i; int j; task main() { DeleteFile("Tempo.txt"); DeleteFile("Data.txt"); DeleteFile("LinVel.txt"); DeleteFile("Theta.txt"); //DeleteFile("AngVel.txt"); CreateFile("Tempo.txt", 1000, fileHandle1); CreateFile("Data.txt", 1000, fileHandle2); CreateFile("LinVel.txt", 1000, fileHandle3); CreateFile("Theta.txt", 1000, fileHandle4); //CreateFile("AngVel.txt", 5000, fileHandle5); SetMotorRegulationTime (10); PosRegEnable(OUT_A,P,I,D); PosRegSetMax (OUT_A, 0, 0); SetSensorLowspeed(S1); // empower the port 1 for sensor DISTNxSendCommand(S1, DIST_CMD_ENERGIZED, DIST_ADDR); // energize the sensor for (i = 0; i < ReadNum; i++) //cycle for calibration { set_point = set_point + DISTNxReadValue(S1, DIST_REG_DIST_LSB, 2, DIST_ADDR); Wait(100); TextOut(10, LCD_LINE3, "Calibrating..."); } ClearScreen(); set_point = ((set_point/ReadNum)*0.001) + 0.2; // give the set point float dato = 0.0; long theta = 0; float AngVel = 0.0; float LinVel = 0.0; float xapCur = 0.0; float xaCur = 0.0 ; float u = 0.0; char Pwr; float time_old = 0.0; float thetaOld = 0.0; float CurPosOld = DISTNxReadValue(S1, DIST_REG_DIST_LSB, 2, DIST_ADDR)*0.001 - set_point; float CurPos = 0.0; float xapOld = 0.0; t0 = CurrentTick(); while (1) { //cycle for regulation for (j = 0; j < FiltNum; j++) { CurPos = CurPos + DISTNxReadValue(S1, DIST_REG_DIST_LSB, 2, DIST_ADDR)*0.001 - set_point; } CurPos = CurPos/FiltNum; // current error X = CurPos ; // current error X //write on file time and error time = (CurrentTick()-t0) * 0.001; theta = MotorRotationCount(OUT_A); thetam = theta * 0.0175 ; AngVel = (thetam - thetaOld)/(time - time_old); LinVel = (CurPos - CurPosOld)/(time - time_old); u = -1 * (K1*CurPos + K2*LinVel + K3*thetam + K4*AngVel); ClearScreen(); NumOut(0, LCD_LINE1, u, false); NumOut(0, LCD_LINE2, CurPos, false); NumOut(0, LCD_LINE3, thetam, false); PosRegSetAngle(OUT_A,u); Pwr = MotorActualSpeed (OUT_A); string tmp1 = NumToStr(time); WriteLnString(fileHandle1,tmp1, bytesWritten1); string tmp2 = NumToStr(X); WriteLnString(fileHandle2,tmp2, bytesWritten2); string tmp3 = NumToStr(u); WriteLnString(fileHandle3,tmp3, bytesWritten3); string tmp4 = NumToStr(thetam); WriteLnString(fileHandle4,tmp4, bytesWritten4); string tmp5 = NumToStr(Pwr); WriteLnString(fileHandle5,tmp5, bytesWritten5); time_old = time; thetaOld = thetam; CurPosOld = CurPos; xapOld = xapCur; CurPos = 0.0; //Wait(20); } DISTNxSendCommand(S1, DIST_CMD_DEENERGIZED, DIST_ADDR); // deenegize the sensor }
Video and Plot
Finally we start simulation and real experiments with NXT and we can see how system react to a disturbance on ball position ( x0 = -0.2 m):
x is equal to zero when the ball is in the center position of the beam, so if a disturbance is introduced the system react to it as shown in the picture below :
Disturbance Rejection Control
PD vs LQR
It was shown how singular controller works in presence of external disturbance, but which of them is the best one?
1)First of all, in PD control I use a second microcontroller (PosRegSetAngle) inside the servomotor which is not necessary in LQR control
2)The setting of PD gains required a lot of trials and experience
3)The PD control doesn’t consider an optimitation of energy in input used during regolation (that’s the big difference from LQR control)
Let's understand better what does it means:
Real Behavior
The previous analysis was only on simulation scenario, but it is possible to reach the same conclusions on real scenario by using nxt lego; The previous simulink model were «ideal» in the sense that it doesn't consider some nonlinearities which are present on real system. Firstly, I use on NXT the same gains obtained from previous ideal simulation:
Of course there is a discrepancy between real and simulated behavior but what I stated previously is still visible. Overshoot and time settling is quite similar but there is a big difference in control effort as I discussed before in the simulation (about energy saving).
Nonlinearities
The difference from ideal simulation and actual reality could be due to several possible reasons:
1)System identification of motor system
2)Deadzones
3)Resolution and accuracy of sensors
4)Discrete system (and not continuos)
5)Friction between ball and beam
It could be possible to implement some of these nonlinearity in the simulink model in order to reach a simulation closer to reality:
By using this new Simulink model, we can observe the nonlinearities also in the simulation:
In my opinion the friction between ball an beam plays important role, especially at the beginning of the regulation where u is nonzero value but the ball is stuck, and this could be bring a sort of delay as picture shown.
Track System Control
Previous experiments show how the system react to an external disturbance; It is possible to implement a Track System Control which means that the system starts in Zero position (all states are equal to 0) and a command on the ball position will send to it. In this way, it is possible to implement also an integrator which will reduce the steady state error ( mainly due to the friction ).
Step Response
Let we see how the system react to a step command of x = -0.2 m :
In this situation , without changing Q and R matrix, the control effort (time settling = 5 s ; overshoot = 1%; umax = 50%) is not accomplished. This is mainly due to the presence of the discrete integrator and the Gain Compensation M which ,at the same time, cancel the steady state error.
Video
Building Instructions
In order to build by yourself the Ball and Beam System, building instructions of the final project design are proposed in the following link: